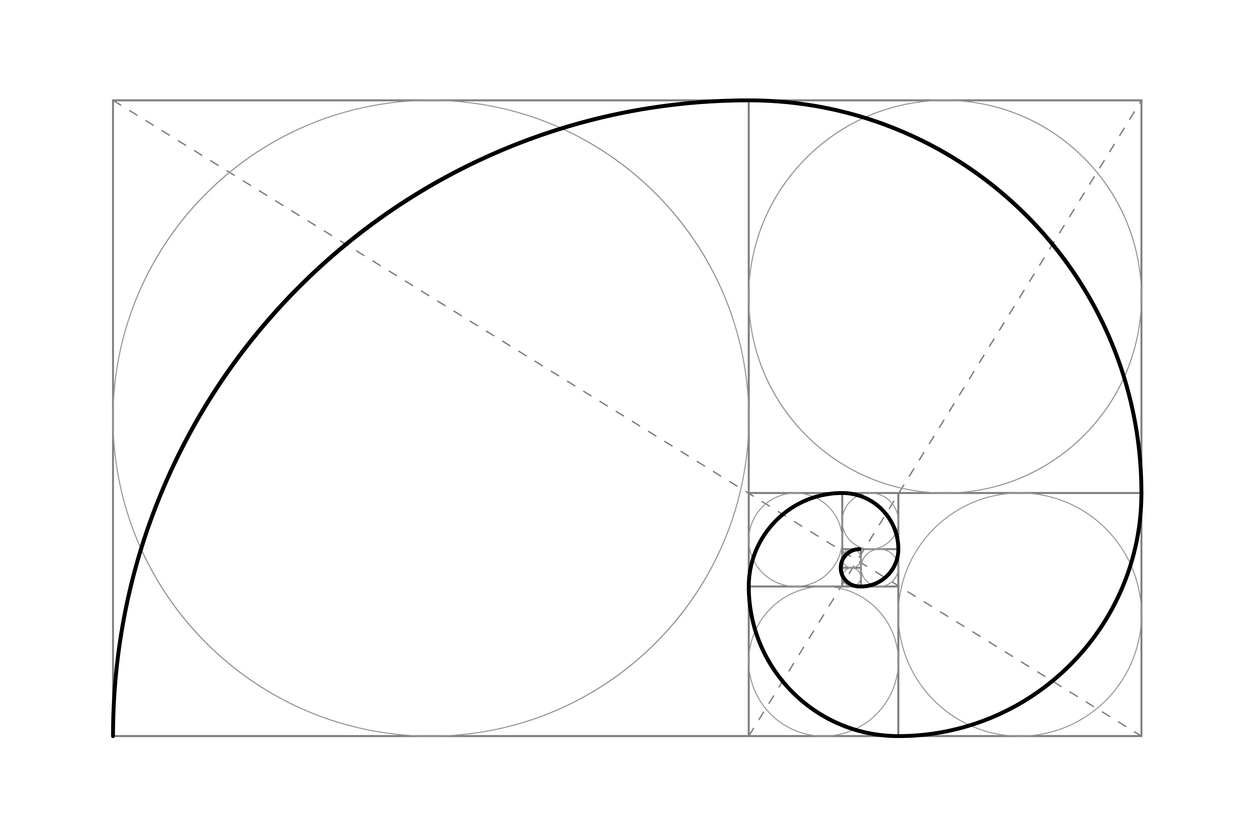
Det gyllene snittet är en välkänt matematiskt förhållande som återkommer i naturen. Det används ofta inom grafisk design och konst, eftersom det upplevs som harmoniskt av människan.
Matematik
Man får fram det gyllene snittet genom att dela en sträcka i en lång del som betecknas a och en kort del som betecknas b. Hela sträckan där a och b kombineras förhåller sig till sträckan a som a förhåller sig till den längre sträckan b. För att beskriva det gyllene snittet matematiskt brukar man använda beteckningen φ, som är den grekiska bokstav som uttalas ”fi”.
Nära knutet till det gyllene snittet är fibonaccisekvensen, som är tal som ingår i en följd av heltal. Varje tal är där summan av de två föregående talen. De första talen Fibonaccis talföljd är 0, 1, 1, 2, 3, 5 osv. Kvoten mellan de tal som följer efter varandra konvergerar mot gyllene snittet. Ju högre upp man kommer i talföljden, desto närmare blir kvoten 1.618, vilket är talet för det gyllene snittet. Som exempel blir 2 delat med 1 2, 3 delat med 2 blir 1,5, 5/3 blir 1.666 och så vidare.
Historia
Den grekiske matematikern och filosofen Pythagoras som levde mellan 570 före Kristus till 495 före Kristus kände redan till det gyllene s nittet; själva upptäckten av det gyllene snittet brukar tillskrivas just honom. Euklides, en grekisk matematiker beskrev detta förhållande i sitt matematiska verk Elementa som framställdes ungefär 300 år före Kristus.
nittet; själva upptäckten av det gyllene snittet brukar tillskrivas just honom. Euklides, en grekisk matematiker beskrev detta förhållande i sitt matematiska verk Elementa som framställdes ungefär 300 år före Kristus.
Under renässansen talades också om detta gudomliga förhållande där man kunde se en total harmoni mellan proportioner och mått. Det gyllene snittet återfanns och användes både i arkitektur, måleri och bildhuggeri.
Även under medeltiden skrevs det om det gyllene snittet i litteratur, av matematikern Luca Pacioli som i sitt litterära verk ”De Divina Proportione” beskrev det gyllene snittet som ett ”gudomligt förhållande”. Boken innehåller också illustrationer av en av världens mest berömda konstnärer, Leonardo da Vinci.
Natur
Många har hittat det gyllene snittet i naturen. Exempel på detta är blombladens placering i solrosor, tallbarren i tallskott, kålväxters blad och rosornas blomblad. Även snäckskal, spiralgalaxer, ansikten, orkaner och DNA-molekyler är ordnade enligt det gyllene snittet. Det kan också uppkomma i fysiken kring svarta hål; det är punkten där hettan ändras och går från positiv till negativ. Fibonacci-talföljden visar sig också tydligt i naturen. Antalet blomblad på en blomma och antalet åsar på en skalad banan brukar vara ett nummer i talföljden.

